2.6 Entropy¶
https://www.youtube.com/watch?v=KoKxlb8R3ew&list=PLMcpDl1Pr-vjXYLBoIULvlWGlcBNu8Fod
Introduction¶
Review¶
In the last section, we calculated the multiplicity of an ideal gas and found that it depends on the number of particles, the volume, and the energy in the system. Like the Einstein solids and paramagnets, there was a very sharp peak around the most likely macrostate.
A General Rule¶
The conclusion from the previous sections seems to be true for all large systems: After a certain period of time, any large system will be found in the macrostate with the greatest multiplicity, with only tiny deviations possible, deviations so small they are impossible to measure.
The Second Law states roughly the same thing: Multiplicity tends to increase over time.
You may have heard it stated many different ways, but the above statement is about the simplest statement you can make about it. Of course, you need to know what “multiplicity” is, at least in this context. This is why we spent the last 5 sections talking about multiplicity and calculating it for various systems.
The Second Law is not fundamental in the same way that energy conservation or force and momentum and such are fundamental. That is, it is not something we assume about the universe without any explanation. It is derived from mathematical probability and counting microstates. It is only tied to reality because it seems reality plays along with the math, and there are random events sorting energy between different things over time.
Keep in mind Schroeder could’ve said “Probability tends to increase over time”, but we’re never interested in the total probability. We can identify the most likely macrostate simply by counting multiplicity and finding its peak.
At this point, this general rule will be invoked as if it were a fundamental law, even though it is a derived law.
One more note: People see that we can explain the Second Law in more fundamental terms, and then they try to ask for explanations of other things, such as “What is charge? What is mass?” and things like that. There are certain things in physics that are not explainable. They just are. Electrons have a charge of -e. Why? Because they do, that’s why. So keep this in mind. Just because this seemingly fundamental law is not fundamental does not mean other things which actually are fundamental are not.
Entropy is a quantity that was discovered before all of the math we went through was understood. Because of this, entropy doesn’t map directly to multiplicity. If we were to use multiplicity, some of the equations would be quite a burden to work with, so we use entropy for its historic quality as well as its elegance.
Entropy uses 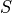 typically, and is related to multiplicity as:
typically, and is related to multiplicity as:
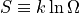
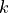 is the familiar Boltzmann constant, and
is the familiar Boltzmann constant, and 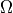 is the
multiplicity.
is the
multiplicity.
Schroeder encourages you to think of S as a unitless number, the log of the multiplicity. However, when you plug it into equations, it has units of the Boltzmann constant, J/K, work per change in temperature.
Einstein Solid, Again¶
Let’s play with entropy as it relates to the Einstein solid. With N
oscillators (from N/3 atoms, typically) and q units of energy, where 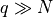 (the “high” temperature limit, which means non-cryogenic),
(the “high” temperature limit, which means non-cryogenic),
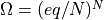 . so:
. so:
![S = k \ln \Omega = k \ln (eq/N)^N = Nk[ln(q/N) + 1]](../../_images/math/c2d70bfc6e3aa0d9785b4708a4561ced00fdf721.png)
Plugging in some typical numbers:
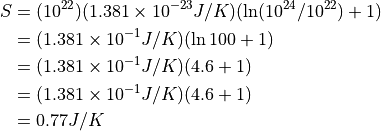
Ways you might incrase the entropy:
Adding more energy
Adding more particles
Increasing the volume
Breaking molecules up
Mixing things together
Disorder¶
Many people think of entropy as “disorder”. This isn’t wrong, but you have to be careful. For instance, a shuffled deck of cards is more disorderly than a new deck, but a cup of ice is less disorderly than a cup of water.
The reason why there is more disorder in the water is because there are many more ways of arranging the water molecules when they are in liquid form and free to move and free to allocate energy in many more ways.
I recommend not using the “disorder” explanation to non-physicists because without a proper understanding of what “disorder” means from the probability perspective, it can lead to confusion.
What I tell people is that what entropy represents is the fact that if you give things enough time to shuffle around, they are going to shuffle around into a particular and predictable way. IE, in a chamber full of gas molecules, they are going to shuffle around until the molecules are more or less evenly spread around, not all on one side of the room. Entropy represents that movement towards that most likely scenario. Things with lower entropy haven’t reached that state yet, while things with maximum entropy have arrived at that state.
Composition of Entropy¶
I’m going to diverge from the text a bit and talk about how we combine the various quantities we have already seen in thermodynamics.
If you take two chambers of gas at the same pressure, and connect them together the pressure remains the same. If they have different pressures, then the higher one will lower and the lower one raise.
If you take two chambers of gas with different volumens, and connect them together, you get a larger chamber with the volume being the sum of the two volumes.
If you take two chambers of gas with a certain number of particles, and connect them together, you get a new chamber of gas with the particles of gas adding up to the sum of the previous numbers.
If you take two chambers of gas with certain temperatures and connect them together, you will find, similar to pressure, that some middle temperature will be reached.
If you take two chambers with a certain amount of internal energy and connect them together, you will get a new chamber with the total internal energy being the sum of the two.
This covers the behavior of those quantities. Some of them add, and some of the do some sort of averaging together. How does entropy behave?
With entropy, you have to go back to how we calculate multiplicites.
If we have two separate chambers of gas, then the total entropy is:
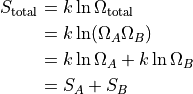
That’s a really nice property to have. Adding is easy. Multiplying not so much.
Now, if we allow the two chambers to interact, we’re going to have to calculate the new maximum multiplicity. Thankfully, this new maximum multiplicity is just the product of the multiplicities when they are apart.
The Second Law of Thermodynamics¶
Thanks to the fact that the log function strictly increases as the number increases, AKA, it is mathematically monotonically increasing, we can make definitive statements about the entropy in relation to the multiplicity, namely, that as multiplicity goes up, so does entropy.
We can reword our original statement about our general observation about multiplicities as:
Any large system in equilibrium will be found in the macrostate with the greatest entropy, aside from deviations which are too small to measure.
Or, in other words:
Entropy tends to increase.
Can Entropy Decrease?¶
Physicists often see the fundamental laws (or in this case, the near-fundamental laws) as a challenge, not a commandment. If I told you that electrons always have -e electric charge, and you were a physicist, you would immediately set about inventing experiments to prove me wrong.
In this case, physicists since entropy was first discovered have tried to figure a way around it. Some of the reasons are entirely selfish (you can create free energy if you violate entropy – we’ll cover that later), but mostly it’s just curiosity.
It seems that is should be possible. After all, if I flip a million coins, I can go through and change all the heads to tails, and arrive at an entirely impossible state.
But when you consider that your body is also subject to the laws of thermodynamics, you can’t help but think that in flipping the coins something has been lost, such that entropy in total has increased. Indeed the energy spent finding and flipping coins ends up as heat or evaporated sweat and carbon dioxide. Doing this on an atomic level would never recover the energy spent doing so, and is a fool’s errand.
So we move to the thought-experiment land. In 1867, James Maxwell wondered about this, and invented a mental model of a tiny being that could open or close a tiny door when it observed molecules moving towards it. It could filter faster molecules to one side, and slower molecules to the other. If such a being could exist, theoretically it is doing no work (since opening and closing a door, without friction, leads to no loss of energy.) This being was later named Maxwell’s Demon, and as far as I can tell, it is theoretically impossible to construct such a creature. I remember back in the 90s people were calculating the limits of computing power usage and determined that even the simplest of calculations would exhaust any net energy increase such a creature would create.
Problems 2.28-2.30¶
2.28 is to calculate the entropy of a deck of cards.
2.29 is to calculate the entropy of 100 energy units shared among two Einstein solids. When calculating the entropy of each macrostate, consider how long such a state would exist over a certain time period.
2.30 is to take 2.22 and calculate the entropy again. It even allows you to try and violate the second law by waiting until a precise moment when you can partition the two solids again.
Entropy of an Ideal Gas¶
We left the multiplicity of an ideal gas in an odd state – with factorials. Let’s rewrite it with Stirling’s approximation.
![\begin{aligned}
S &= k \ln \Omega \\
&= k \ln \left [
\frac{1}{N!}
\frac{V^N}{h^{3N}}
\frac{\pi ^{3N/2}}{(\frac{3}{2}N)!}
(2mU)^{3N/2}
\right ] \\
&= k \ln \left [
\frac{(2 \pi m)^{3N/2}}{N! h^{3N} (3N/2)!}
V^N
U^{3N/2}
\right ] \\
&= k \left [
\ln (2 \pi m)^{3N/2}
- \ln N!
- \ln h^{3N}
- \ln (3N/2)!
+ \ln V^N
+ \ln U^{3N/2}
\right ] \\
&= k \left [
(3N/2) \ln (2 \pi m)
- (N \ln N - N)
- 3N \ln h
- [(3N/2) \ln (3N/2) - (3N/2)]
+ N \ln V
+ (3N/2) \ln U
\right ] \\
&= N k \left [
(3/2) \ln (2 \pi m)
- (\ln N - 1)
- 3 \ln h
- [(3/2) \ln (3N/2) - (3/2)]
+ \ln V
+ (3/2) \ln U
\right ] \\
&= N k \left [
\ln V
- \ln N
+ (3/2) \ln (2 \pi m)
+ (3/2) \ln U
- (3/2) \ln h^2
- (3/2) \ln (3N/2)
+ 1
+ (3/2)
\right ] \\
&= N k \left [
\ln \frac{V}{N}
+ (3/2) \ln \frac{
2 \pi m U
}{
(3N/2) h^2
}
+ \frac{5}{2}
\right ] \\
&= N k \left [
\ln \frac{V}{N}
+ \ln \left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2}
+ \frac{5}{2}
\right ] \\
&= N k \left [
\ln
\left (
\frac{V}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2} \right )
+ \frac{5}{2}
\right ] \\
\end{aligned}](../../_images/math/b533df9144af73060c183d7a0fbf095ceade7fa3.png)
This is the Sackur-Tetrode equation.
A mole of Helium at room temperature and pressure has a volume of
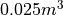 and an internal energy of
and an internal energy of 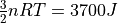 . It’s
entropy is:
. It’s
entropy is:
![\begin{aligned}
S &=
N
k
\left [
\ln
\left (
\frac
{V}
{N}
\left ( \frac{
4
\pi
m
U
}{
3
N
h^2
} \right )^{3/2}
\right )
+ \frac{5}{2}
\right ] \\
S &=
(6.022 \times 10^{23})
(1.381 \times 10^{-23} \text{J}/\text{K})
\left [
\ln
\left (
\frac
{(0.025\ \text{m}^3)}
{(6.022 \times 10^{23})}
\left ( \frac{
4
\pi
(4 \times 1.673 \times 10^{-27} \text{kg})
(3700\ \text{J})
}{
3
(6.022 \times 10^{23})
(6.626 \times 10^{-34}\ \text{J}\cdot\text{s})^2
} \right )^{3/2}
\right )
+ \frac{5}{2}
\right ] \\
S &=
(8.316\ \text{J}/\text{K})
\left [
\ln
\left (
(4.151 \times 10^{-26}\ \text{m}^3)
\left ( \frac{
(3.111 \times 10^{-22}\ \text{kg}\cdot\text{J})
}{
3
(6.022 \times 10^{23})
(4.390 \times 10^{-67}\ \text{J}^2\cdot\text{s}^2)
} \right )^{3/2}
\right )
+ \frac{5}{2}
\right ] \\
S &=
(8.316\ \text{J}/\text{K})
\left [
\ln
\left (
(4.151 \times 10^{-26}\ \text{m}^3)
\left ( \frac{
(3.111 \times 10^{-22}\ \text{J}^2 \cdot \text{s}^2/\text{m}^2)
}{
(7.931 \times 10^{-43}\ \text{J}^2\cdot\text{s}^2)
} \right )^{3/2}
\right )
+ \frac{5}{2}
\right ] \\
S &=
(8.316\ \text{J}/\text{K})
\left [
\ln
\left (
(4.151 \times 10^{-26}\ \text{m}^3)
(3.923 \times 10^{20}\ \text{m}^{-2})^{3/2}
\right )
+ \frac{5}{2}
\right ] \\
S &=
(8.316\ \text{J}/\text{K})
\left [
\ln
\left (
(4.151 \times 10^{-26}\ \text{m}^3)
(7.769 \times 10^{30}\ \text{m}^{-3})
\right )
+ \frac{5}{2}
\right ] \\
S &=
(8.316\ \text{J}/\text{K})
\left [
\ln (3.225 \times 10^5)
+ \frac{5}{2}
\right ] \\
S &=
(8.316\ \text{J}/\text{K})
(
12.68
+ 2.5
) \\
S &=
(8.316\ \text{J}/\text{K})
(15.18) \\
S &= 126.3\ \text{J}/\text{K}) \\
\end{aligned}](../../_images/math/b6e449f0905e8a7c8ffee35f36f402b254d77100.png)
Typically, we aren’t really interested in the total entropy, but how the entropy changes under changing circumstances.
If we were to increase N, V, or U, then we would see the entropy increase monotonically for an ideal gas.
Let’s look at what happens when we change V and keep N and U constant.
![\begin{aligned}
\Delta S &= S_f - S_i \\
&= N k \left [
\ln
\left (
\frac{V_f}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2} \right )
+ \frac{5}{2}
\right ]
- N k \left [
\ln
\left (
\frac{V_i}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2} \right )
+ \frac{5}{2}
\right ] \\
&= N k \left [
\ln
\left (
\frac{V_f}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2} \right )
+ \frac{5}{2}
- \ln
\left (
\frac{V_i}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2} \right )
- \frac{5}{2}
\right ] \\
&= N k \left [
\ln
\left (
\frac{V_f}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2} \right )
- \ln
\left (
\frac{V_i}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2} \right )
\right ] \\
&= N k \ln
\left (
\frac{
\frac{V_f}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2}
}{
\frac{V_i}{N}
\left ( \frac{
4 \pi m U
}{
3N h^2
} \right ) ^{3/2}
}
\right )
\\
&= N k \ln \left ( \frac{V_f}{V_i} \right ) \\
\end{aligned}](../../_images/math/c531793cc4f6c6d9efa16bdb3419ade3072cdd9a.png)
So if the volume increases, then the entropy has increased, but if the volume decreased, then the log is negative and the entropy has decreased.
Note that we have to keep N and U fixed. N fixed means that no gas is entering or leaving. And U fixed means that the temperature is held constant – it’s an isotherm. So this is the case where we allow a gas to expand or contract under constant pressure as we add or remove heat. Putting heat energy into a system increases its entropy, while drawing heat out decreases it. There is an important relationship between heat and entropy we’ll look at in chapter 3.
An interesting case arises if we create a chamber with a gas on one side and a vacuum on the other. If we puncture the barrier, then gas will freely flow into the vacuum. No work was done since there is no force being applied, there was no change in internal energy (since heat did not flow in or out) but the volume expanded. In this case, we have created entropy out of literally nothing!
Problems¶
2.31: Derive the Sackur-Tetrode equation (which I did above. Please don’t copy my work.)
2.32: Calculate the entropy of a 2D ideal gas from 2.26.
2.33: Calculate for a mole of argon gas. Why did the entropy increase? (How does entropy differ between two ideal gasses of the same temperatuer and pressure but different masses? Why does multipliticy increase with more mass?)
2.34: Show the relationship
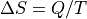 for the quasistatic
isothermal expansion. (Isotherm: temperature is constant. quasistatic: We’re
not moving faster than the speed of sound in the substance.) This is an
important formula in the next chapter and applies to more than ideal
gases.
for the quasistatic
isothermal expansion. (Isotherm: temperature is constant. quasistatic: We’re
not moving faster than the speed of sound in the substance.) This is an
important formula in the next chapter and applies to more than ideal
gases.2.35: At what temperature does the entropy turn negative according to the Sackur-Tetrode equation? We’ll explore cryogenics in chapter 7.
2.36: This one is just for fun.
Entropy of Mixing¶
Entropy also increases as we have things mix together.
We can calculate the increase in entropy by treating the two things as completely separate even though they are thoroughly mixed.
If we have a chamber with a membrane splitting it into two equal chambers, and
there is a different gas in each chamber, then if we were to pierce the
membrance and allow them to mix the entropy of both sides would increase by
a factor of 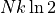 . The total increase in entropy is just
. The total increase in entropy is just 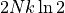 , where
, where 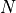 is the number of particles in one side, or if you
prefer
is the number of particles in one side, or if you
prefer 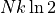 if N is the total number of particles in both sides.
if N is the total number of particles in both sides.
This is called the entropy of mixing.
If both chambers were full of the same gas, then there would be no change at all of the entropy. Mixing helium and helium gives you helium, after all. This might seem a bit counterintuitive – after all, didn’t the multiplicity increase? Indeed, it did, but not by a very large number, just a large number, and so compared to the total multiplicity, nothing changed.
Another way to think of this is to start with a full chamber of helium, and
then to add argon. In this case, the total entropy would be
 . The entropy of the
helium and argon are pretty similar – but a small difference arises due to the
difference in mass. Effectively, the entropy doubled when the argon was added.
. The entropy of the
helium and argon are pretty similar – but a small difference arises due to the
difference in mass. Effectively, the entropy doubled when the argon was added.
However, if you added helium instead of argon, the entropy wouldn’t simply
double. Both N and U must double, and cancel each other out inside the square
root of the cube part. But inside the log, N appears under the V and this does
double, lowering the log. The difference between simply doubling the entropy
and what actually happens is 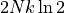 . This is the entropy gained
by adding argon rather than helium. Or the entropy not gained when adding
helium to helium rather than argon to helium. This value is the entropy of
mixing – the entropy that arises simply because you are mixing two different
kinds of things together, as opposed to adding more of the same stuff.
. This is the entropy gained
by adding argon rather than helium. Or the entropy not gained when adding
helium to helium rather than argon to helium. This value is the entropy of
mixing – the entropy that arises simply because you are mixing two different
kinds of things together, as opposed to adding more of the same stuff.
In short, entropy is remembering not just how much stuff you have, how energetic it is, how big it is, but also whether or not that stuff is made of the same stuff or different stuff. And the entropy due to having mixed things is very significant.
If you go back to where the N under the V came from, you’ll recall that it came from the fact that when you have multiple particles that are the same, they are completely indistinguishable from each other and so you must be careful not to count their configuations twice. You must divide by N! to ensure that you’re counting them once. However, if you CAN distinguish the particles because they are actually different, then you do need to count the various configurations.
Indeed, if you tried to do the math for entropy allowing every particle to be distinguishable, you’d get a modified formula without an N in the denominator. The net effect of this is that if you inserted a partition into a chamber, you would reduce the entropy just by dividing it up! This would have profound consequences – to the math at least, and would mean a violation of the second law every time someone added a partition. This is known as the Gibbs paradox, and we don’t have a good way to explain it away with a simple experiment, but we certainly don’t like it.
Problems¶
2.37: mixing things that aren’t the same number.
2.38: More on mixing.
2.39: Calculate entropy if all helium atoms were distinguishable.
Reversible and Irreversible Processes¶
If a physical process increases the total entropy in the universe, then that process cannot happen in reverse, since it would violate the second law. These processes are therefore called “irreversible”.
Processes which do not increase the entropy are reversible and so we call them that.
In reality, reversible processes are purely theoretical. We can get close, but there is always a little bit of entropy created no matter what we do.
While you can “reverse” so-called irreversible processes (IE, a refrigerator), doing so requires spending entropy somewhere else, usually more than what it cost in the first place.
We’ll talk a lot more about this in future chapters.
There is sometimes some subtlety to these processes, so it isn’t immediately clear which ones are and are not reversible. For instance, if you were to allow a gas to suddenly expand, that would create entropy. But a quasistatic expansion or compression may not lead to an increase in entropy. Quasistatic means that the work done on the gas is the same as the pressure times the change in volume – in other words, no heat flowing in or out. But we need to exercise caution and count all the ways that entropy might change in the process before we can be confident it is a reversible process.
You might imagine at the quantum level that the compression of a gas is like squeezing the wave functions. If you do it too quickly, the particles will jump up an energy level, increasing the total energy units, but if you do it slow enough, there won’t be enough energy to cause any to jump up. The state of the system remains essentially the same, even though the volume has changed.
You might hear someone say “reversible heat flow”, which sounds like nonsense, especially given what we have just learned. But take anything to an extreme, you’ll find some sort of contradictory behavior. Indeed, two systems which differ by microscopic amounts of temperature will exchange energy in a way that doesn’t increase the total entropy. Indeed, most processes, in the infinitessimal limit, are reversible. The tiniest changes due to the tiniest differences really don’t change the entropy at all. But these changes can accumulate where entropy does change and thus in the macro-level are irreversible, even though they aren’t quite irreversible in the micro-level.
When we look at the world around us, and the processes that we readily see occuring, two facts become apparent: 1. That the universe is increasing in entropy, and will eventually reach some maximum state, the so-called “heat death of the universe”. But more interesting is the fact that the universe came from somewhere with a lower entropy, and therefore there must have been some sort of beginning of it all in some insanely low entropy state.
These sorts of questions aren’t really the purview of physics, but they are interesting philosophical questions that arise because of the observations we have made in physics. How you choose to answer them is up to you, and has no bearing on what we do with what we know right now in physics.
Problems¶
2.40: Try to explain these processes using the things we have learned here. IE, the entropy of mixing, how entropy is related to the number of particles, the temperature, the volume, etc…
2.41: This one is a “fun” problem. One way to think of this: If you had to spend entropy, how would you prefer to do it? As for me, I enjoy eating a good meal; much more enjoyable than being in a car accident.
2.42: This is a fun guided exercise to get close to a result that Stephen Hawking derived in 1973 concerning Black Holes.
Closing Quote¶
Reminds me of the scene where Dr. Evil goes back in time to the 1960s and asks the US government to give him a billion dollars. They laugh at him.

